Documentation > Tutorials
The simplest numerical experiments that can be done with such a stochastic model are:
Warning: The default value for @code{mySeed} must be removed from the model task, otherwise it will overwrite the seeds generated by the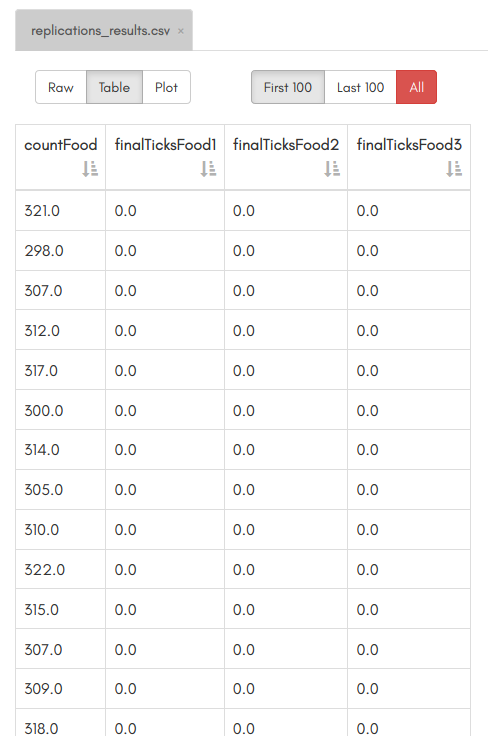 You won't have the same numbers as above, since the random seed won't be the same.
However, you should have the same column names and 100 lines of results: one for each model execution.
You won't have the same numbers as above, since the random seed won't be the same.
However, you should have the same column names and 100 lines of results: one for each model execution.
Rate parameters
We use the
The script is the following: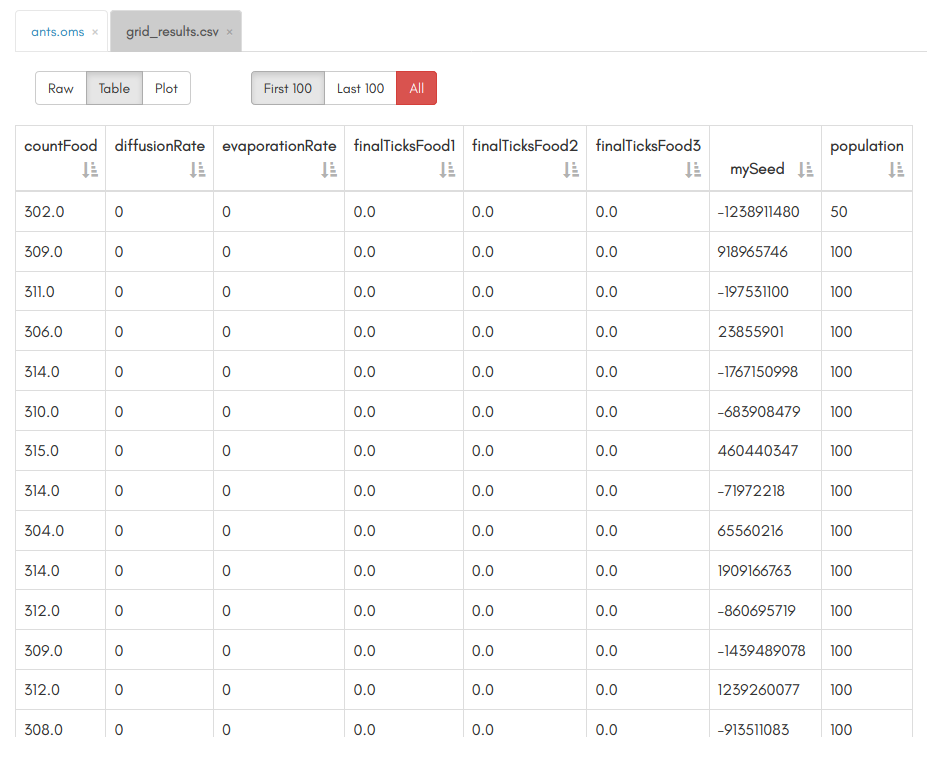
Content:
Overview 🔗
In this tutorial, you will learn how to prepare and run an experiment, in order to explore a simple model. The toy model is @i{Ants.nlogo}, since we already know how to import and run it from the previous tutorial.The simplest numerical experiments that can be done with such a stochastic model are:
- run the model several times with the same parameter values to understand the statistics of its behavior,
- run the model with different parameter values to have a glimpse of their influence on the model's behavior.
Replicating the Ants model 🔗
A stochastic model ran several times with the same parameter set will give different outputs. It is the case of the Ants model we used in the previous tutorial. In order to repeat easily a model execution and concatenate the results, OpenMOLE provides theReplication task.
Workflow 🔗
As the model has a random seed parameter namedmySeed, it can be passed to the Replication task as an argument.
The task will then attribute seeds itself to each model run (necessary for exact reproducibility).
Warning: The default value for @code{mySeed} must be removed from the model task, otherwise it will overwrite the seeds generated by the
Replication task.
// Input values
val mySeed = Val[Int]
val diffusionRate = Val[Int]
val evaporationRate = Val[Int]
val population = Val[Int]
// Output values
val countFood = Val[Double]
val finalTicksFood1 = Val[Double]
val finalTicksFood2 = Val[Double]
val finalTicksFood3 = Val[Double]
// NetLogo commands list
val launch = List(
"setup",
"go ;;You should set your stopping criteria here instead"
)
// NetLogo task
val antsTask = NetLogo6Task(
workDirectory / "ants.nlogo", // netlogo file
launch, // launching commands
seed = mySeed // set the random seed
) set (
inputs += diffusionRate mapped "diffusion-rate",
inputs += evaporationRate mapped "evaporation-rate",
inputs += population mapped "population",
outputs += countFood mapped "count-food",
outputs += finalTicksFood1 mapped "final-ticks-food1",
outputs += finalTicksFood2 mapped "final-ticks-food2",
outputs += finalTicksFood3 mapped "final-ticks-food3",
// Default values. Can be removed if OpenMOLE Vals are set by values coming from the workflow
diffusionRate := 21,
evaporationRate := 9,
population := 125
)
// Define the replication task
val replications = Replication(
evaluation = antsTask, // the model to run
seed = mySeed, // the seed variable
sample = 100 // the number of model executions
)
// Workflow
// Note: here we use a hook which gathers all the outputs of the replication and writes them into a csv file
replications hook (workDirectory / "replications_results")
Results 🔗
Once the execution is over, refresh your workspace by clicking on the second-to-last icon on the left of the GUI (circle with two arrows). A new file will appear named replications_results.omr, this is the file that our workflow created, containing the replication results! You can click on it. You won't have the same numbers as above, since the random seed won't be the same.
However, you should have the same column names and 100 lines of results: one for each model execution.
You won't have the same numbers as above, since the random seed won't be the same.
However, you should have the same column names and 100 lines of results: one for each model execution.
Exploring the parameter space 🔗
The results from the previous experiment gave us information about the statistical distributions of outputs, their covariance structure, etc.), we know more about the role of stochasticity in this setting of the model. However, we do not know anything about the influence of the input parametersdiffusionRate, evaporationRate, and population on these outputs.
This is exactly the aim of sensitivity analysis and exploration methods which are integrated into OpenMOLE.
Workflow 🔗
Let's illustrate a simple experiment of a grid search of the parameter space. Each input parameter will take a finite number of values within a defined interval.Rate parameters
diffusionRate and evaporationRate are between 0 and 100, and let's say we consider ant populations of sizes comprised between 50 and 150.
With a step of 50 for each interval, the complete grid has a size of 27 (3x3x3) parameter sets to explore.
We use the
DirectSampling method, which takes as arguments the sampling itself (i.e. the grid we just defined with the parameter values), and the model to evaluate.
Instead of running one instance of the model for each parameter set of our grid, which would not make much sense because of the model's stochasticity we discussed above, we will replicate each one 100 times with the Replication task.
This way, statistics can then be computed for each parameter set.
The script is the following:
// Input values
val mySeed = Val[Int]
val diffusionRate = Val[Int]
val evaporationRate = Val[Int]
val population = Val[Int]
// Output values
val countFood = Val[Double]
val finalTicksFood1 = Val[Double]
val finalTicksFood2 = Val[Double]
val finalTicksFood3 = Val[Double]
// NetLogo commands list
val launch = List(
"setup",
"go ;;You should set your stopping criteria here instead"
)
// NetLogo task
val antsTask = NetLogo6Task(
workDirectory / "ants.nlogo", // netlogo file
launch, // launching commands
seed = mySeed // set the random seed
) set (
inputs += diffusionRate mapped "diffusion-rate",
inputs += evaporationRate mapped "evaporation-rate",
inputs += population mapped "population",
outputs += countFood mapped "count-food",
outputs += finalTicksFood1 mapped "final-ticks-food1",
outputs += finalTicksFood2 mapped "final-ticks-food2",
outputs += finalTicksFood3 mapped "final-ticks-food3"
)
// Define the replication task
val replications = Replication(
evaluation = antsTask, // the model to run
seed = mySeed, // the seed variable
sample = 100 // the number of model executions
)
// Define the grid sampling task
val exploration = DirectSampling(
evaluation = replications, // here we evaluate the Replication task for each value of the sampling
sampling =
(diffusionRate in (0 to 100 by 50)) x
(evaporationRate in (0 to 100 by 50)) x
(population in (50 to 150 by 50))
)
// Workflow
exploration hook (workDirectory / "grid_results")
Results 🔗
In the same way we did before, after refreshing your workspace you will find a new file named @i{grid_results.omr}, containing the results of our grid sampling. You can then use the results to better understand how your model behaves.